Discussion 3

Bullets

• Rasterization pipeline (in discussion 3)
  • Vertex processing
  • Triangle processing
  • Rasterization
  • Fragment processing
    • Simple shading: Blinn-Phong Reflection Model
  • Framebuffer operations
• Cubic Hermite Interpolation
• Catmull-Rom Interpolation
  • Using Cubic Hermite interpolation
• Bézier curves
  • Evaluation
    • de Casteljau algorithm
    • Algebraic formula
      • Berstein polynomials (can be derived from de Casteljau algorithm)
  • Continuity
• Bézier surfaces
  • Evaluation
    • Separable de Casteljau algorithm
    • Algebraic formula
  • Continuity
• Geometry representations (covered in discussion 4)
  • Explicit
    • Point cloud
    • Polygon mesh
    • Subdivisions
    • NURBS
  • Implicit
    • Level sets
    • Algebraic surface
    • Distance functions
    • etc.

---

Rasterization pipeline

• Vertex processing
• Triangle processing
• Rasterization
• Fragment processing (Blinn-Phong Reflection Model)
• Framebuffer operations

Real world example

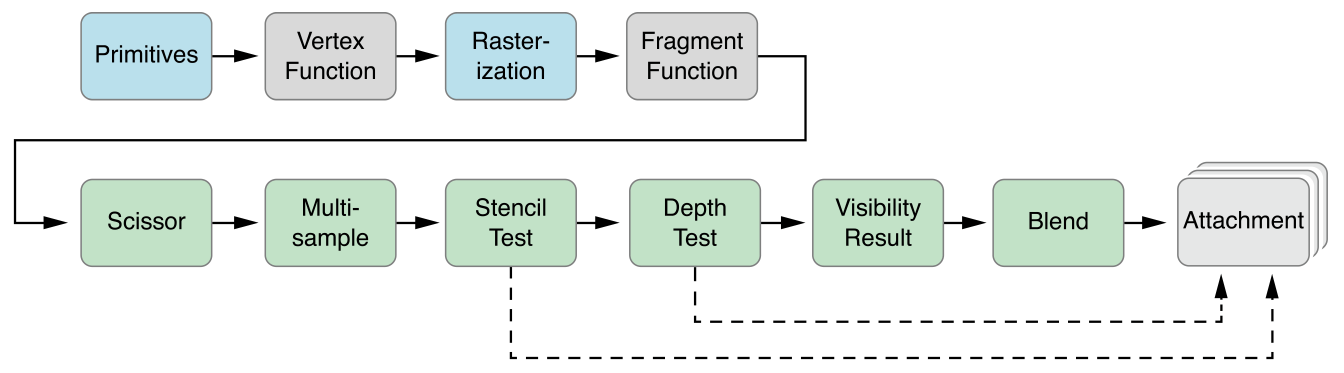
🍿 If time permits: Demo per-vertex & per-fragment lighting with Metal

Cubic Hermite Interpolation

Hermite basis functions

\begin{align} P(t) & = \begin{bmatrix}t^3 & t^2 & t^1 & t^0\end{bmatrix} \begin{bmatrix}a \\ b \\ c \\ d\end{bmatrix} \\ & = \begin{bmatrix}H_0(t) & H_1(t) & H_2(t) & H_3(t)\end{bmatrix} \begin{bmatrix}h_0 \\ h_1 \\ h_2 \\ h_3\end{bmatrix} \\ & = \begin{bmatrix}H_0(t) & H_1(t) & H_2(t) & H_3(t)\end{bmatrix} \begin{bmatrix}P(0) \\ P(1) \\ P'(0) \\ P'(1)\end{bmatrix} \end{align}

Catmull-Rom Interpolation

Plug-in Cubic Hermite Interpolation

\begin{align} P(t) & = \begin{bmatrix}H_0(t) & H_1(t) & H_2(t) & H_3(t)\end{bmatrix} \begin{bmatrix}P(0) \\ P(1) \\ P'(0) \\ P'(1)\end{bmatrix} \\ & = \begin{bmatrix}H_0(t) & H_1(t) & H_2(t) & H_3(t)\end{bmatrix} \begin{bmatrix}0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ -1/2 & 0 & 1/2 & 0 \\ 0 & -1/2 & 0 & 1/2\end{bmatrix} \begin{bmatrix}P_0 \\ P_1 \\ P_2 \\ P_3\end{bmatrix} \end{align}

Bézier curves & surfaces

🖍 Board work on de Casteljau's algorithm & Berstein polynomial